この本のTOPへ
Statcel4 とは…
目次
重複計測・一元配置分散分析法
全部で51個あります。
A市の20歳代の女性の健康診断のデータから、「身長」、「体重」について、基本統計量を求め、さらにヒストグラムを描いてデータの分布状況を確認しなさい。
example02(正規性の検定)A市の20歳代の女性の健康診断のデータから、「身長」についてデータの正規性を危険率5%で検定しなさい。
example03(母分散が既知のときの母平均の検定)20歳代の女性の血液中の血色素数の平均値は13.8(g/dl)で、標準偏差は 1.1(g/dl)ある。A市の20歳代の女性の健康診断のデータの「血色素数」の平均値は13.5(g/dl)であった。A市の20歳代の女性の血色素数の平均値は13.8(g/dl)より小さいとみなせるかどうか、分散は一般の20歳代の女性と変わりなかったとして危険率5%で検定しなさい。
example04(母分散は未知のときの母平均の検定)20歳代の女性の血清総コレステロール(TC)の平均値は180(mg/dl)である。A市の20歳代の女性の健康診断データの「TC」の平均値は183.2(mg/dl)で、標準偏差は26.1(mg/dl)であった。A市の20歳代の女性のTCの平均値は180(mg/dl)より大きいとみなせるかどうか危険率5%で検定しなさい。
example05(母平均が既知のときの母分散の検定)一般女子の血液中の赤血球数は平均値は435(万/mm3)で標準偏差は31.5(万/mm3)である。A市の20代の健康診断のデータの「赤血球数」の平均値は438.9(万/mm3)で、標準偏差は28.4(万/mm3)であった。A市の20歳代の女性の赤血球数の標準偏差は31.5(万/mm3)より小さいとみなせるかどうか、平均値は一般女子と変わらなかったとして危険率5%で検定しなさい。
example06(母平均が未知のときの母分散の検定)B市の新生児20人の体重を調べたところ、次の結果がえられた。一般新生児の体重の標準偏差は460g である。 B市の新生児の体重の分散は460^2gとみなせるかどうか危険率5%で検定しなさい。
example07(母分散が既知のときの母平均の推定)B市の新生児20人の体重から、一般新生児の体重の平均値を信頼度99%で推定しなさい。一般新生児の体重の標準偏差460gである。
example08(母分散が未知のときの母平均の推定)20歳代の男性の最高血圧を測定したところ、次のデータが得られた。このデータから20歳代の一般男性の最高血圧の平均値を信頼度95%で推定しなさい。
example09(母平均が既知のときの母分散の推定)A市の健康診断のデータの「赤血球数」から、一般女子の赤血球数の分散を信頼度99%で推定しなさい。一般女子の赤血球数の平均値は435(万/mm3)である。
example10(母平均が未知のときの母分散の推定)A市の健康診断のデータの「TG」(中性脂肪)から、20歳代の一般女性のTGの分散はどの範囲にあるか。信頼度99%で推定しなさい。
example11(F検定)血液中の蛋白値Pを測定したところ次のような結果が得られた。男女間で蛋白値Pの分散が等しいかどうか危険率5%で検定しなさい。
example12(スチューデントの t 検定)血液中の蛋白値Pを測定したところ次のような結果が得られた。男女間で蛋白値Pに差があるかどうか危険率5%で検定しなさい。
example13(ウェルチ t 検定)女性をある条件のもとに A、B2 群に分け血色素数(g/dl)を調べたところ、次のようなデータが得られた。 A群とB群の血色素数に差があるかどうか危険率1%で検定しなさい。
example14(マン・ホイットニ検定(大標本の場合))20歳代と30歳代の男性の飲酒傾向を調べたところ次のようなデータが得られ、集計すると次の分割表にまとめられた。年代によって飲酒傾向に違いがあるかどうか危険率5%で検定しなさい。

AおよびBの条件のもとで、ある疾患について陰性か陽性かを調べたら次の結果が得られた。集計すると次の分割表にまとめられた。条件によって疾患の発生に違いがあるかどうかを危険率5%で検定しなさい。
植物中に含まれる生理活性物質Bの加熱による変化を調べるために加熱処理前後の活性を測定したところ次のデータを得た。加熱処理によって活性が変化するといえるかどうか危険率5%で検定しなさい。
example17(ウィルコクソン符号付順位和検定(大標本の場合))30人の患者に A、B2種類の睡眠薬を与えて、睡眠時間の延長を測定したところ次の結果が得られた。両薬に差があるかどうか危険率5 %で検定しなさい。
example18(ウィルコクソン符号付順位和検定(小標本の場合))10人のアレルギー性皮膚炎の患者に、A、Bの2種類の外用薬を異なる部位に同時に塗って薬の効果に差があるかどうか調べた。効果の判定を5段階(1:悪化、2:不変、3:やや有効、4:有効、5:著効)で評価して次の結果が得られた。薬の効果に差があるかどうか危険率5%で検定しなさい。
example19(バートレット検定)赤血球溶血毒素 Aの活性を調べるため、ヒト、ウサギ、ウシの血球を用いて実験を行ったところ次のデータを得た。ヒト、ウサギ、ウシの3群の溶血活性の分散は均一であるかどうか危険率5%で検定しなさい。 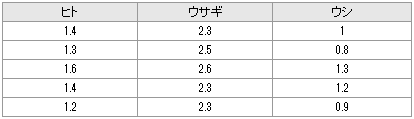
赤血球溶血毒素Aの活性を調べるため、ヒト、ウサギ、ウシの血球を用いて実験を行ったところ次のデータを得た。ヒトとその他の種との間で溶血活性に差があるといえるかどうか危険率5%で検定しなさい。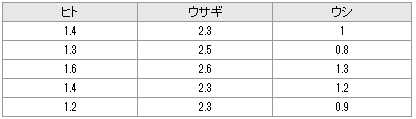
ある薬物を3種類のラットに投与した効果を5段階評価で調べたところ、次のデータを得た。ラットの種類によって薬物の効果に差があるかどうか危険率5%で検定しなさい。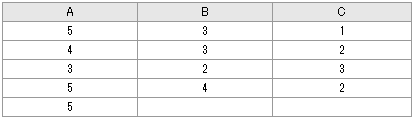
10人の患者に降圧剤を投与して1ヶ月ごとに平均血圧(mmHg)を測定したら、次のようなデータが得られた。投与期間によって差があるのかき危険度5%で検定しなさい。
example23(クェード検定)10人のアレルギー性皮膚炎の患者に、A、B、Cの3種類の外用薬を異なる部位に同時に塗って薬の効果に差があるか調べた。
効果の判定を5段階(1:悪化、2:不変、3:やや有効、4:有効、5:著効)で評価して次の結果が得られた。薬の効果があるかどうか危険率5%で検定しなさい。
ある企業の入社面接で、15人の志願者に対して4人の審査員の合否判定が次のようになりました(合格1、不合格0)。審査員の判定に差があるかどうか危険率5%で検定しなさい。
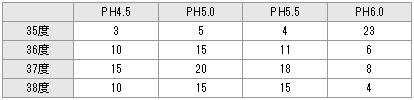
example25(繰り返しのない二元配置分散分析法)ある酵素の至適反応条件を調べるために、一定量の基質を加え、温度、PH を変化させて生成物の量を測定したところ、次のデータが得られた。
-
- 温度の変化で生成物の量に差があるかどうか
- PHの変化で生成物の量に差があるかどうかについて危険率5%で検定しなさい。
ある疾患の治療薬 A、B、C について、5人の医師 A、B、c、d、eが評価し、評価の高い順に1から3までの順位をつけたところ次のデータがえられた。
-
- 医師の評価に差があるかどうか
- 3種類の治療薬の評価に差があるかどうかについて危険率5%で検定しなさい。
ある疾患の3種類の治療薬 A、B、Cの効果を調べるために患者に投与し、その効果を性別、治療薬別に集計したところ、次のようなデータが
-
- 性別と治療薬に交互作用があるかどうか
- 性別により効果に差が認められるかどうか
- 治療薬により効果に差が認められるかどうか
について危険率5%で検定しなさい。
同じ種類のラットを A、B2群に分け、A群には実験薬を、B群には対照薬を連日経口投与し、ある反応を1週間後、2週間後、3週間後に測定した。
-
- 薬の種類と投与期間に交互作用があるかどうか
- 薬の種類によって反応に差どうか
- 投与期間によって反応に差があるかどうか
について危険率5%で検定しなさい。
example29(多重比較検定:Tukey-Kramer法、Bonferroni/Dunn法)赤血球溶血毒素Aの活性を調べるため、ヒト、ウサギ、ウシの血球を用いて実験を行ったところ次のデータを得た。一元配置分散分析を用いて検定を行ったところ、ヒトとその他の種との間で溶血活性に差があることが判明した(Example20)。多重比較検定によりどの水準とどの水準に差が認められるかどうかを 危険率5%で検定しなさい。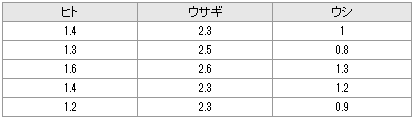
ある疾患の 3種類の治療薬 A、B、C の効果を調べるために患者に投与し、その効果を性別、治療薬別に集計し、得られたデータに基づき危険率5%で繰り返しのある二元配置分散分析法を用いて検定を行ったところ、
-
- 性別と治療薬に交互作用がある
- 性別により効果に差が認められる
- 治療種により効果に差が認められる
ことが把握できた(詳しくは example24)。水準間の差を調べたいので、性別と治療薬を組にして一元配置分散分析法を用いて検定したところ、水準間に差があることが判明した。多重比較検定によりどの水準とどの水準に差が認められるかどうかを危険率5%で検定しなさい。
example31(多重比較検定(Dunnett法))ラットを対象にある疾患の3種類の治療薬 A、B、Cの効果を調べるために、投与しない群(対照群)と治療薬 A、B、Cを投与した群とで値を測定し、次の結果を得た。多重比較検定により、対照群とどの治療薬を投与した群に差が認められるか危険率5%検定しなさい。
example32(多重比較検定(Williams法))ある薬物は血中レベルを上げ、高用量での有効性は認められているが、安全性にやや問題がある。もっと低用量でも有効であって、さらに有害事象の発生率が低下することを確かめるために、用量を1日当たり0μg/kg(Control)、0.05μg/kg、0.5μg/kg、1.0μg/kg、5.0μg/kgをそれぞれラット10匹ずつに2週間投与した。その後、血中レベルを測定して次の結果を得た。この薬物をどのくらい投与したら有効性が認められるか、危険率5%で検定しなさい。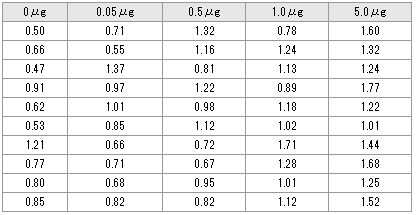
ある薬物を3種類のラットに投与した効果を5段階評価で調べてところ、次のデータを得た。クラスカル・ワーリス検定を用いて検定を行ったところ、ラットの種類によって薬物の効果に差があることが判明した(例題21、121頁)。ラットのどの種類とどの種類に差が認められるかノンパラメトリック多重比較検定のSteel-Dwass法を用いて判定しなさい。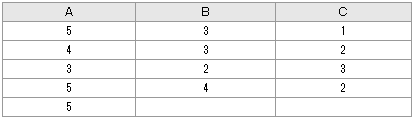
ある新薬剤Aの効果を調べるために、現行の薬剤Bを対照薬とし、また伝統的な薬剤Cも比較対照とした3薬剤の比較試験を行った結果、次のようになりました。薬剤Aは薬剤Bまた薬剤Cに比べて優れているといえるかどうかノンパラメトリック多重比較検定のSteel法を用いて検定しなさい。
薬剤Aの用量が増加すればある特性値の減少がみられるかどうかに関心があります。薬剤Aの用量を5段階に設定し(A1はプラセボ投与群)、データはそれぞれの投与群からランダムに採取し、ある特性値を10段階評価して、次の結果を得ました。プラセボ投与群と有意差のあるのは第何群以降と言えるかノンパラメトリック多重比較検定のShirley-Williams法を用いて検定しなさい。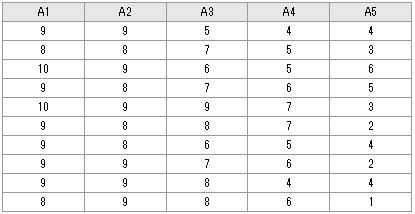
A市の20歳代の女性の健康診断のデータから、「身長」、「体重」、「TC」に相関関係があるかどうかを危険率5%で検定しなさい。
example37(スピアマンの順位相関係数検定(大標本の場合))A市の20歳の女性の健康診断で肝機能のGOTとGTPの相関関係を危険率5%で検定しなさい。
example38(スピアマンの順位相関係数検定(小標本の場合))健常人の血中中性脂肪値(TG)と空腹時血漿グリコース値(FPG)を調べたところ次の結果が得られた。TGとFPGの相関関係を危険率5%で検定しなさい。
example39(単回帰分析)A市の20歳代の女性の健康診断の「身長」と「体重」のデータから、20歳代の女性の体重を身長から推定する回帰直線を求めなさい。さらに、この回帰直線が予測に役立つかどうか、また体重を予測するのに身長は必要な変数であるかどうかを危険率5%で検定しなさい。
example40(重回帰分析)次のデータは25人の健康な男性についてある検査をした結果です。測定値 A1、A2、A3、A4 は安静状態の数値、測定値Bと測定値Cは運動負荷をかけたあとのある種の測定値です。測定値 A1、A2、A3、A4と測定値Bのデータから測定値Cを予測する回帰関数を求めなさい。さらに、この回帰関数が予測に役立つかどうか危険率5%で検定しなさい。
example41(変数選択-重回帰分析)example40のデータを用いて、目的変数の予測に役立つ説明変数を選択しなさい。
A市の20歳代の女性の健康診断の「身長」と「体重」のデータから、20歳代の女性の体重を身長から予測する整次多項式回帰関数を求めなさい。次数を変えていくつか関数を求め、最適な回帰関数を求めなさい。さらに、この回帰関数が予測に役立つかどうか危険率5%で検定しなさい。
example43(2 × 2 分割表 χ2独立性の検定)ある腫瘍に対する2つの治療法 A、Bの効果を比較するために、それぞれの治療を行った患者の一定期間後の生存の有無を調べたところ、次のような結果が得られた。治療法により生存率が異なるといえるかどうか危険率5%で検定しなさい。
example44(2 × 2 分割表 フィッシャーの直接確率計算法)AおよびBの条件のもとで、ある疾患について陰性か陽性かを調べたら次の結果が得られた。集計すると次の分割表にまとめられた。条件によって疾患の発生に違いがあるかどうかを危険率5%で検定しなさい。
猛暑であったといわれる 1994年の大阪の 7月、8月の真夏日(日最高気温が30℃以上)の日数を平年と比較すると次のような結果が得られた。1994年の大阪の夏は平年に比べて本当に猛暑であったといえるかどうか危険率1%で検定しなさい。
example43で得られたデータを臨床病期で、病床2期、病床3期、病床4期に分けると次のようになった。それぞれについて、2 × 2分割表のχ2 独立性の検定を行った結果、病床 2期と病床 3期では治療法により生存率に有意な差は認めらなかたっかが、病床4期では危険率5%で有意な差が認められた。 病床2期、病床3期、病床4期の 2 × 2 分割表を合わせて治療法と生存率の関連性を危険率5%で検定しなさい。
example47(m × n 分割表 χ2 独立性の検定)大学生男女100人に各自の社交性についてのアンケート調査を行い、兄弟構成をもとに集計して次のような結果が得られた。社交性と兄弟構成に関連があるかどうか危険率 5%で検定しなさい。ただし、社交性については、社交的:Sociable(S)、普通:Medium(M)、非社交的:Unsocialbe(U)に分類し、兄弟構成については、一人子(A)、長子(B)、末子(C)、中間子(D)に分類した。 
ある新薬Aの効果を調べるために、対照薬Bを使って薬効試験を行った結果は次のようになった。両薬の効果に差があるかどうか、危険率5%で検定しなさい。
男性の健康診断で血液型と飲酒傾向を調べたところ次のようなデータが得られ、集計すると次の分割表にまとめられた。血液型と飲酒傾向に関連があるかどうか危険率5%で検定しなさい。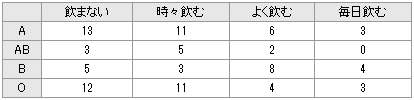
男性の健康診断の身長と体重から肥満度をBMI(Body Mass Index)を計算し、肥満度を次の4段階で評価して、20歳代、30歳 代、40歳代の年齢別に集計し分割表にまとめた。年齢と肥満度の関連性を危険率5%で検定しなさい。 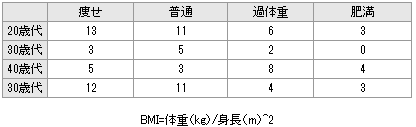
ある種のがん患者に対して、治療法Aと治療法Bを行って、生存時間(日)を調べたところ、次のような結果が得られた。それぞれの治療法による生存率を求め、治療法によって生存率に差があるかどうかを危険率5%で検定しなさい。